Ein besonders einfaches Modell
Im folgenden werden wir eine ersten Versuch unternehmen, die Konvergenzeingeschaften evolutionärer Algorithmen auszutesten. Ganz besonderer Augenmerk soll auf die Eignung von Problemen mit sehr vielen Parametern gelegt werden. Dabei soll nicht nur im numerischen Experiment die Eignung untersucht werden, sondern auch gleichzeitig nach Formeln gesucht werden, die die Konvergenzeigenschaften analytisch beschreiben.
Als praktischer Anwendungsfall dient die "Optimierung" von Fotos. Am Anfang stand die vermutlich mehr als naive Idee, man könne ein verwackeltes Foto dadurch verbessern, indem man einen Ansatz über das korrekte Bild sowie die Wackelbewegung der Kamera macht und beide Annahmen zum Gegenstand einer vielparametrigen Optimierung macht. Ob das funktionieren wird, ist erst einmal ungewiss. Vielleicht steht am Ende dieser Betrachtungen ja tatsächlich eine entsprechende Software zur Verfügung. Vielleicht wissen wir am Ende aber nicht nur, dass es nicht geht, sondern auch warum es nicht gehen kann und niemals gehen wird. So lange wir noch nichts von der Sache verstehen, lassen wir das mit der wackelenden Kamera erst mal weg.
Jenseits dieses möglichen Nutzens, sind Fotos aber auch in anderer Hinsicht ein lohnenwertes Untersuchungsobjekt:
- Das Problem ist hochparameterisch. Bei einem Bild mit den typischen 24 Bit pro Pixel und einer Größe von gerade einmal 500 x 333 Bildpunkten hat man es bereits mit fast 4 Mio Bits an zu optimierender Information zu tun.
- Bilder sind anschaulich. Der Fortschritt der Optimierung lässt sich unmittelbar visuell überprüfen. Die einzelnen Zwischenschritte zu einem „Daumenkino“ verbunden machen die Evolution besser erfahrbar als es mit öden Tabellen oder Kurven möglich wäre.
Brutale Vereinfachungen
Am Anfang stehen erst einmal einige brutale Vereinfachungen. Wir benutzen im folgenden eine sehr einfache Form evolutionärer Algorithmen.
- Fitness: Ein zentraler Begriff der Evolutionstheorie ist die Fitness, die in der Biologie die überlebens- und Fortpflanzungswahrscheinlichkeit eines Organismus beschreibt. Wir benutzen eine extrem einfache Fitnessfunktion, indem wir lediglich zählen, wieviele Bits eines „Individuums“ mit denen des Zielfotos übereinstimmen. Im weiteren wird diese simple Fitness von mir auch als Ähnlichkeit bezeichnet werden.
- Selektion: Für den Anfang gehen wir davon aus, dass sich von einer Generation nur das Individuum mit der höchsten Fitness vermehrt. Ich nenne das die „the winner takes it all“ Selektion.
- Mutation: Beim Erzeugen einer neuen Generation wird zunächst der Gewinner der Selektion kopiert und eine vorher festgelegte Zahl von Mutationen ausgeführt. Da wir unser Problem als die Optimierung eines sehr großen Bitfeldes betrachten, ist eine Mutation nichts anderes als das Umkippen eines Bits von 0 auf 1 oder umgekehrt.
- Ursuppe: Wir starten immer mit einer solchen. D.h. alle Bits sind in einem zufälligen Zustand.
- Cross-over, diploide Chromsomen etc.: Noe, noch zu kompliziert und noch nicht verstanden. Vielleicht später.
Noch mehr Vereinfachungen
Es geht noch einfacher. Der kleinste evolutionäre Algorithmus liegt dann vor, wenn es pro Generation nur eine einzige Mutation gibt. Es seien:
- Gesamtzahl der zu optimierenden Bits
- Zahl der korrekten Bits („good“)
- Zahl der falschen Bits („bad“)
- Zahl der Individuen in einer Population
The lonely wolf – Populationsgröße 1
Als allerersten Fall versuchen wir eine Populationsgröße von 1 in Formeln zu fassen. Das heißt, wir haben ein einzelnes Individuum, das bei der Erzeugung seines einzigen Nachkommen eine einzelne Mutation erfährt. Die Wahrscheinlichkeit, dass es bei einem einzigen Versuch zu einer Verbesserung kommt, liegt bei
während die Wahrscheinlichkeit für eine Verschlechterung bei
liegt. Wohin entwickelt sich dieses System? Wenn die Wahrscheinlichkeit für eine Verbesserung größer als 50% ist kann man erwarten, dass im Schnitt mehr Verbesserungen als Verschlechterungen auftreten. Ansonsten geht es mit der Qualität des Ergebnisses eher abwärts als aufwärts.
Ärgerlich! Verbesserungen sind nur zu erwarten, wenn weniger als die Hälfte aller Bits korrekt sind. Sind mehr als die Hälfte aller Bits bereits korrekt, dann geht es abwärts. Mit nur einem einzelnen Individuum kommt man über die Qualität einer Ursuppe mit 50% aller Bits im korrekten Zustand nicht hinaus!
Größere Populationen
Was passiert nun, wenn man die Populationsgröße von 1 auf erhöht? Will heißen: Von dem gleichen Vater der gleichen Mutter dem gleichen Elter werden mehrere mutierte Versionen erzeugt. Wie wahrscheinlich ist es jetzt, dass wenigstens eine dieser Varianten eine Verbesserung darstellt? Zunächst die Wahrscheinlichkeit, dass mal hintereinander keine Verbesserung erzielt wird. Sie ist
Die Wahrscheinlichkeit, dass es wenigstens einmal Verbesserung gibt, ist dann der verbleibende Rest von den 100%, also
Kommen wir nun mit Individuen über das Niveau der Ursuppe (50% der Bits ok) hinaus? Wie wir bereits vorher gesehen haben, definiert die 50% Wahrscheinlichkeit für eine Verbesserung den Grenzwert des Erreichbaren einer gegen unendlich strebenden Zahl von Generationen
Grenzwert der 1-Mutation-Optimierung in Abhängigkeit von der Populationsgröße bzw. als absolute Größe. Eine kleine Wertetabelle:
| Populationsgröße | Erreichbarer Grenzwert |
|---|---|
| 1 | 50,00% |
| 2 | 70,71% |
| 3 | 79,37% |
| 4 | 84,09% |
| 5 | 87,06% |
| 6 | 89,09% |
| 7 | 90,57% |
| 8 | 91,70% |
| 9 | 92,59% |
| 10 | 93,30% |
| 20 | 96,59% |
| 30 | 97,72% |
| 40 | 98,28% |
| 50 | 98,62% |
| 60 | 98,85% |
| 70 | 99,01% |
| 80 | 99,14% |
| 90 | 99,23% |
| 100 | 99,31% |
Welche Populationsgröße benötigen wir mindestens, um ein bestimmtes Qualitätsmaß zu erreichen? Einfaches Umstellen unserer Formel genügt:
| Geforderter Grenzwert | Erforderliche Populationsgröße |
|---|---|
| 50,00% | 1 |
| 60,00% | 1,3569154489 |
| 70,00% | 1,9433582099 |
| 80,00% | 3,1062837195 |
| 90,00% | 6,578813479 |
| 91,00% | 7,3496149582 |
| 92,00% | 8,3129504141 |
| 93,00% | 9,5513375094 |
| 94,00% | 11,2023055836 |
| 95,00% | 13,513407334 |
| 96,00% | 16,9797480183 |
| 97,00% | 22,7565730628 |
| 98,00% | 34,3096184915 |
| 99,00% | 68,9675639365 |
| 99,10% | 76,6692575921 |
| 99,20% | 86,2963600238 |
| 99,30% | 98,6740464467 |
| 99,40% | 115,1776088858 |
| 99,50% | 138,2825729861 |
| 99,60% | 172,9399900374 |
| 99,70% | 230,7023130491 |
| 99,80% | 346,2269010495 |
| 99,90% | 692,8005491785 |
Geschwindigkeit der Optimierung
Um das Fortschreiten der Optimierung zu berechnen, gehen wir davon aus, dass die Wahrscheinlichkeit der Änderung der Ähnlichkeit zwischen zwei Generationen entspricht, also der Differenz aus und :
Diese Differenzengleichung erlaubt eine rekursive Berechnung des Fortschritts der Iteration. Möglicherweise kann man sie auch analytisch in Form einer Reihe berechnen.
Computerprogramm
Nach diesem kurzen Ausflug in die Theorie wenden wir uns jetzt dem eigentlichen Problem, der Erzeugung von Bildern zu. Obwohl die eingangs geschilderte Erzeugung von Bilddateien eigentlich die Verwendung einer Low-Level-Sprache wie C nahelegen sollte, wird im folgenden ein Programm in einer ordentlichen Sprache, nämlich JAVA entwickelt. Die Performance von C und JAVA programmen unterscheiden sich nicht nennenswert. In Java ist aber alles einfacher zu realisieren, weil man nicht dauernd gegen die Primitivität der Sprache anprogrammieren muss.
Das Programm erledigt in der ersten Ausbaustufe die folgenden Arbeiten:
- Einlesen der Optimierungsparameter voni der Kommandozeile
- Einlesen eines Bildes, das per evolutionärem Algorithmus rekonstruiert werden soll
- Erzeugung einer Ausgangspopulationen als Ursuppe
- Selektion geeigneter Individuen für die nächste Generation
- kontinuierliches Speichern von Zwischenzuständen
Insbesondere der letzte Punkt verdient besondere Beachtung. Größere Optimierungsprobleme können durchaus mehrere Millionen Generationen erfordern. Irgendwann werden sie ihren Computer auch für was anderes benötigen, müssen die Berechnung unterbrechen und zu einem späteren Zeitpunkt fortsetzten. Oder es geht ihnen so, wie mit: Als ich in den frühen Neunziger Jahren erste Gehversuche mit einem genetischen Algorithmus (zur Optimierung von Spiralbohrern) auf einem VAX-Cluster durchführte, hatte ich es mit Laufzeiten von mehr als einer Woche zu tun. Ärgerlichweise hatte ich alle Daten waren nur im RAM gehalten und irgendwann nach der erstenWoche fiel während des Wochenendes der Strom aus. Remember what Al Lowe said: "Save early, save often". Häufiges Speichern Not, wir benutzen es auch um den Verlauf der Optimierung zu dokumentieren.
Details zu dieser Bastellösung (Quellcode, Bedienungsanleitung) finden sich hier: Implementierung
Das Bild
Das Bild ist das Ziel der Optimierung und dient gleichzeitig auch dazu den Optimierungsverlaufs plakativ darzustellen. Prinzipiell würde jedes x-beliebige Pixelmuster diesen Zweck erfüllen,. Optisch lässt sich der Fortschritt auch mit einem definierten Muster verfolgen. Ausreichend und genaugenommen am besten geeignet, wäre eine einfarbige Fläche, Weiß oder Schwarz. Weil es aber einfach besser aussieht, wird doch ein willkürlich ausgesuchtes Bild verwendet. Die Abmessungen diese Bildes sind 500 x 333 Pixel mit 24 Bit Farbtiefe. Das Optimierungsproblem umfasst also
Das Original des Bildes wird hier nicht wiedergegeben, weil ich nicht mehr sagen kann, woher es stammt. Vermutlich mit meiner Handykamera entstanden, aber möglicherweise aber auch sonst woher. Mit Google finde ich es jedenfalls nicht mehr. Daher werde ich hier nur die Bilder wiedergeben, die das Evolutionsprogramm algorithmisch erzeugt hat. Sie stellen letztlich eigenständige Schöpfungen dar.
Bislang ist es mir noch nicht gelungen, den Ablauf der Optimierung als Funktion der Populationsgröße und Nummer der Generation als geschlossene Gleichung darzustellen. Die theoretische Vorhersage erfolg daher mittels der weiter oben wiedergegebenen rekursiven Berechnungsgleichung. Das Ergebnis is in Bild 1 wiedergegeben (dünne Linien). Die überlagerten dicken farbigen Linien geben das Ergebnis unserer evolutionären Bilderzeugung dar. Die Linien sind praktisch deckungsgleich. Die animierte Darstellung zeigt gleichzeitig noch wie sich bei den verschiedenen Parametern nach und nach das eigentliche Bild aus einem chaotischen Pixelhaufen herausentwickelt.
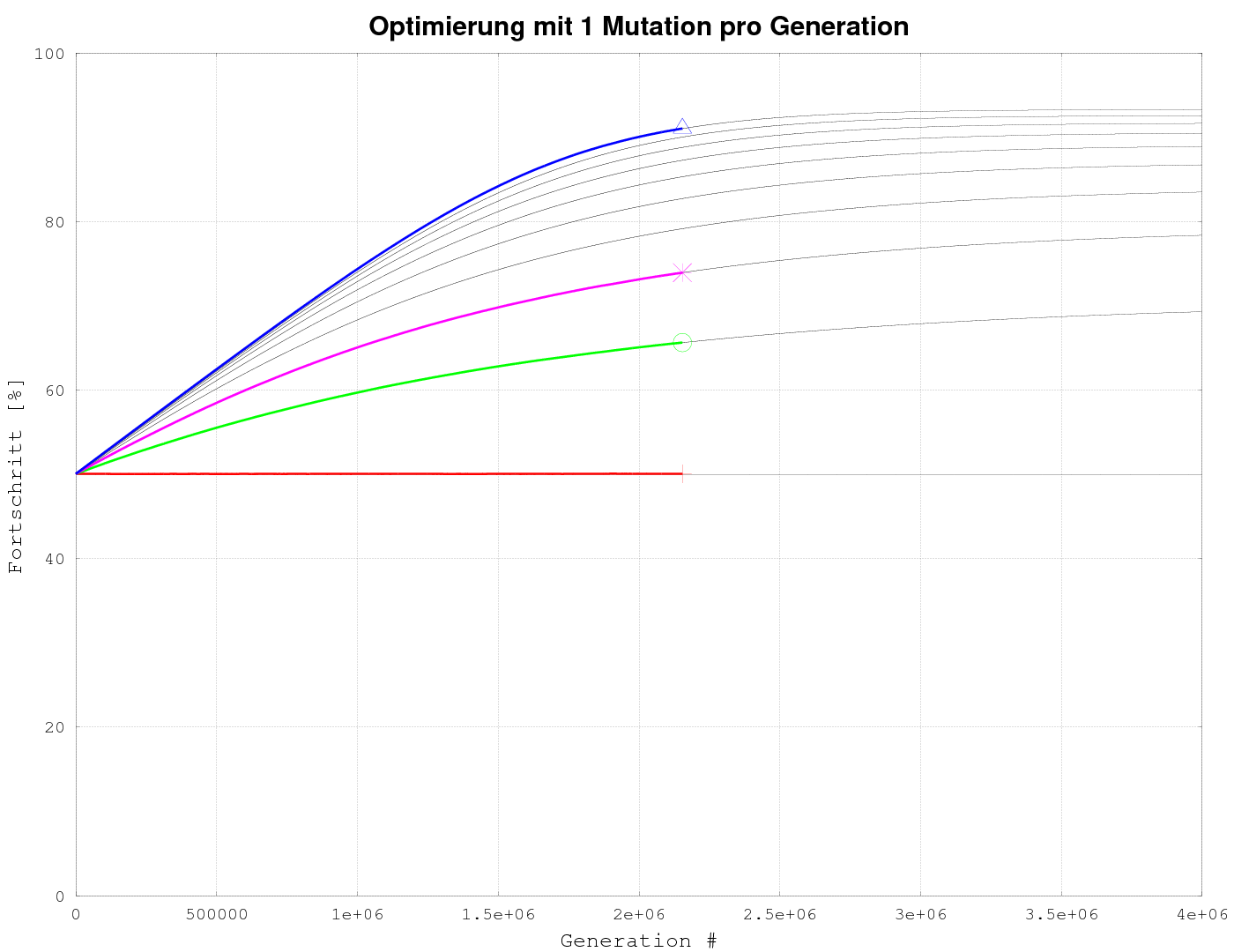
Das Ganze gibt es auch als animierte Darstellung: animierte Darstellung
Leider klappt das Abspielen momentan nicht mit jedem Player. Das multimediale schweizer Taschenmesser vlc kann es.
Geschwindigkeit und Kosten der Optimierung
Wir können jetzt ausrechnen, wie schnell die Optimierung in Abhängigkeit von der Populationsgröße abläuft und wie gut das Ergebnis bestenfalls ausfallen wird. In unserem Beispiel mit den ca. 4 Mio Bits brauchen wir ungefähr 2 Millionen Generationen um uns ungefähr bis zum Grenzwert vorzutasten. Irgendwo habe ich mal gelesen, dass sich Bakterien unter guten Bedingungen alle 20 Minuten teilen können. Ignorieren wir vorübergehend einmal, dass sich ein Bakterium immer nur in zwei Kopien aufspaltet, dann sind das ungefähr 40 Mio. Minuten oder 76 Jahre. Recht lange für einen Menschen, erdgeschichtlich aber recht überschaubar.
Aber ist das wirklich die Geschwindigkeit der Optimierung? Ist das wirklich der Fortschritt pro Generation? Immerhin unterscheidet sich der zu treibende Aufwand deutlich, je nachdem ob man in jeder Generation 2 oder 10 Individuen hinsichtlich ihrer Fitness bewertet. Sofern wir die Auswertung der Fitnessfunktion parallel durchführen können, mag der Fortschritt pro Generation tatsächlich die Geschwindkeit sein. Es ist die gleiche Situation wie in der belebten Welt. Die Lebewesen existieren nebeneinander her. Während das eine ins Gras beißt, beißt das andere in die Gazelle. Bei der Simulation auf einem sequentiell arbeitenden Digitalrechner sieht die Sache ganz anders aus. Die Rechenzeit skaliert hier proportional mit der Populationsgröße. Und Parallelität hin oder her: Die Kosten des Verfahrens resultieren aus der Anzahl von Auswertung der Fitnessfunktion eines jeden einzelnen Individuums und sind damit proportional zur Populationsgröße.
Vergleichen wird das miteinander. Zuerst noch einmal die Geschwindigkeit in Abhägigkeit von der Generationszahl. Scheinbar schnell geht es mit einer besonders großen Populationsgröße. Trägt man aber jetzt die gleichen Daten über der Zahl der ausgewerteten Individuen auf (indem man die Nummer der Generation mit der Populationsgröße multipliziert), sieht es plötzlich ganz anders aus. Umso größer die Population ist, umso kleiner ist die Geschwindigkeit!
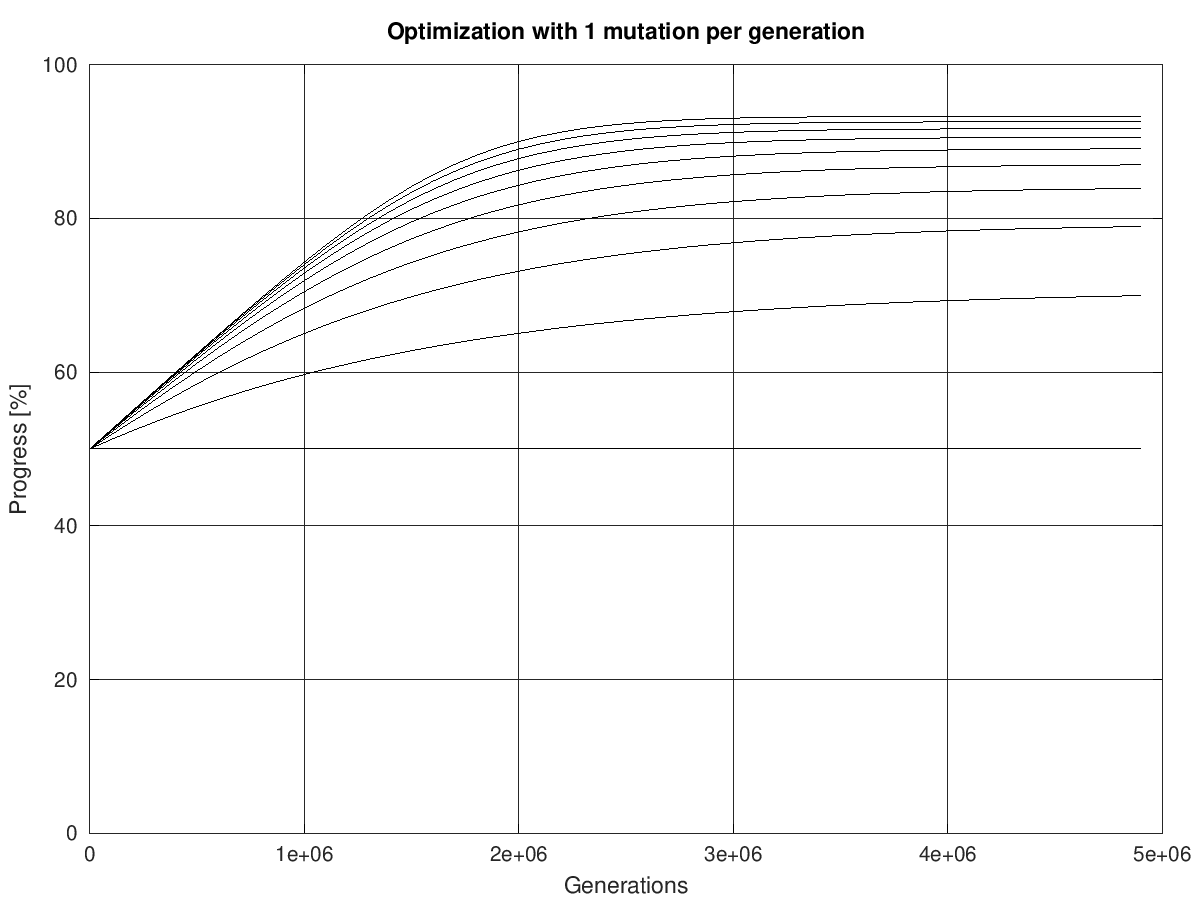

Ein adaptiver Algorithmus?
Wäre es nicht eine gute Idee, den Mitteleinsatz bei der Optimierung zu minimieren? Ein Ansatz könnte darin bestehen mit der kleinstmöglichen Populationsgröße zu starten. Da dem Verfahren relativ schnell die Puste ausgeht, muss irgendwann die Populationsgröße irgendwann erhöht werden.
Woran merken wir, dass dem Algorthmus "die Puste ausgeht"? Wir ermitteln in jeder Generation ob sich die Fitness gegenüber der Vorgängergeneration verbessert oder verschlechtert hat. Hat es in den letzten soundsovielen Generationen keine ausreichende Menge an Verbesserungen gegeben, wird es Zeit die Populationsgröße um eins zu vergrößern.
Die Hoffnung ist, dass wir uns damit immer am linken oberen Rand unserer Kurvenschar in Bild 3 bewegen. Der praktische Beweis steht noch aus.
Bei einem Genom von vier Millionen Bits dürfte es eher unwahrscheinlich sein, dass sich die Biologie auf eine einzige Mutation pro Generation beschränken wird. Aber wie wirkt es sich aus, wenn der Zufall härter zuschlägt? Lesen sie weiter im dritten Teil Mehrere Mutationen pro Generation.