Über das Infinite Monkey Theorem oder die Wichtigkeit von Vererbung

Wir beginnen mit einer Spielerei, einem Gedankenexperiment, das gerne als Argument gegen die Evolutionstheorie herangezogen wird. Im Original besagt das Infinite Monkey Theorem ungefähr: Wenn Schimpansen unendlich lange zufällig auf einer Schreibmaschine herumtippen, müssten doch irgendwann im Textfluß sämtliche Werke Shakespeares erscheinen. Es gibt Varianten des Theorems, etwa dass es doch sehr, sehr unwahrscheinlich und damit faktisch unmöglich sei, dass ein über einen Schrottplatz hinwegfegender Hurrikan aus den herumliegenden Schrottteilen eine Boeing 747 Jumbo Jet zusammensezten wird.

Analysieren wir die Shakespeare-Variante einmal mathematisch. Der Einfachheit halber gehen wir davon aus, Shakespeare habe nur in Grossbuchstaben geschrieben und wir ignorieren großzügig, dass es in seinen Texten auch noch Leerzeichen und Interpunktionszeichen gibt. Somit gibt es für jedes einzelne Zeichen 26 verschiedene Möglichkeiten. Die Wahrscheinlichkeit, dass ein einzelnes per Zufall bestimmtes Zeichen den korrekten Buchstaben annimmt, ist:

$p = \frac{1}{26}$

Betrachten wir mehr als ein einzelnes Zeichen, dann "versechundzwanzigst" sich mit jedem weiteren Zeichen die Zahl der Möglichkeiten und die Wahrscheinlichkeit geht entsprechend immer weiter zurück. Bei $n$ Zeichen beträgt die Wahrscheinlichkeit, dass alle Zeichenposition den passenden Buchstaben eines Shakespeare-Textes angenommen haben nur noch:

$p = {(\frac{1}{26})}^{n}$

Wir alle wissen, dass das praktisch ausgeschlossen ist. Aus blankem Zufall allein entsteht niemals Ordnung, niemals etwas anderes als Durcheinander. Es ist schlicht und einfach zu unwahrscheinlich. Wäre das die Grundidee der Evolution, dann wären wir hier tatsächlich am Ende. Aber: So ist es eben nicht, Evolution ist nicht einfach nur Zufall. Denn dieses Argument ignoriert so ziemlich das wichtigste an der belebten Natur. Die Wesen vermehren sich von Generation zu Generation und ihre Eigenschaften werden mehr oder weniger vererbt. Irgendwie erwartet jeder (auch Evolutionsgegner), dass ihm seine Kinder ähnlich sehen (sieht ein Kind dem Nachbarn ähnlich, so spricht man von Umwelteinfluss).

Es ist aber auch selbstverständlich, dass Kinder ihren Eltern nicht vollständig gleichen. Eine fast vollständige Gleichheit zweier Menschen ist eher selten. So selten, dass es in manchen Sprachen sogar einen eigenen dafür Begriff gibt: Im Deutschen nennt man das Phänomen Zwillinge. Mittlerweile verstehen wir einigermaßen viel von den molekularen Grundlagen der Vererbung. Wir verstehen sogar so viel, dass viele bereits Angst vor dem Missbrauch unseres Wissens in Form genetisch veränderter Lebewesen haben.

Gehen wir also zurück zum Beispiel unseres Affen, der "unendlich" lange an seiner Schreibmaschine arbeitet und vergleichen es mit einer zugegeben sehr vereinfachten Version dessen, wovon die Evolutionstheorie handelt. Die Modellvererbung ist arg vereinfach (wir werden das später kritisch beleuchten). Wir verwenden erst einmal nur einen winzig kleinen Ausschnitt aus "Hamlet" von William Shakespeare. Eine blanke, englischsprachige Textversion kann man sich aus dem Internet herunterladen, z.B. von http://www.gutenberg.org/files/1524/1524-0.txt. Dabei fällt mir gerade ein: Ist Shakespeares Urheberrecht an "Hamlet" eigentlich zwischenzeitlich verfallen? Shakespeare hatte die Rechte bis 75 Jahre nach seinem Tod inne. Da er aber gar nicht gelebt haben soll, kann er gar nicht verstorben sein. Also was nun...

T O B E O R N O T T O B E

Das ist die vermutlich bekannteste Stelle des Stücks. Wie versprochen habe ich zur Vereinfachung nur Großbuchstaben benutzt und sowohl Leerzeichen als auch Interpunktionszeichen weggelassen.

Auftritt Affe (mit dem Zieltext übereinstimmende Buchstaben sind hervorgehoben):

R F R Y Y M F N F Y I C S

Das ist jetzt nicht unbedingt Shakespeare, noch nicht einmal ein Tweet von Donald Trump. Aber der Affe schreibt ja fleißig weiter...
K P X P N U U X K E C B S

Jetzt landet der Affe immerhin einen ersten Treffer! Ein "B" ist schon da. Aber der Affe haut immer noch in die Tasten.
B C U M Y K I T P M X C O

Blöd, dass unser Affe immer wieder von vorne beginnt. Denn das "B" im dritten Anlauf schon wieder weg.
C G G L X B E B I Z O B F
C Q R W K R I K N D F E B
S T D P R Y I A E V J W Y
R V Q O G K B U H Z Z K L
T W O K Z I P Q R C Y W V
I B H O I E D F N P P G Z
V F R N B O T D V U F S P
N V O T H B W Z I J R D C
A J I G Q R K K T L D G F
F Y Y M A I Z F D C I W M
S W Y K C L Q I S P H C I
D E A F A W C S D Y L C G

So setzt sich das leider bis ins Unendliche fort. Das ist eine mathematische Gewissheit (hatten wir ja gerade ausgerechnet) und deshalb lassen wir den Affen jetzt in Frieden. Es gibt für die 13 Zeichen aus einem Vorrat von 26 Buchstaben ungefähr $2,5 \cdot 10^{18}$ Möglichkeiten. Richtige Zeichen kommen, aber richtige Zeichen verschwinden auch fast sofort wieder. Mehr als zwei korrekte Zeichen finden sich selten in einer Zeile.

Jetzt der Auftritt der Evolution oder zumindest von etwas, was der Evolution deutlich näher kommt, als ein tippender Affe: Unsere Einfach- Evolution fängt nicht jedes mal beim Punkte null, sie arbeitet mit VERERBUNG. Dass gleich beim ersten Versuch bereits ein Buchstabe korrekt ist, ist dem blanken Zufall zuzuschreiben. Aber dieser Zufallstreffer wird im nachfolgenden nicht mehr verworfen, sondern weiterbenutzt, weil es korrekt ist und sich daher bewährt hat. Deswegen haben wir in der zweiten Zeile bereits zwei korrekte Zeichen, obwohl wir auch in dieser lediglich einen Zufallstreffer gelandet haben. 15 Runden später haben wir 7 von 13 Buchstaben korrekt bestimmt.

L R T J Q U Q I K Y X B A
I E B K E I W L S J W B Y
U L B R Z C R C A F J B I
B N B Y N P O V T R P B T
S T B Q L Z E S T B O B B
T M B H A N B T T Q O B M
T T B E G E G B T Y O B R
T X B E M G V R T Y O B S
T M B E L R T P T F O B Q
T P B E B R W A T E O B B
T Y B E A R G Z T C O B X
T G B E Z R E X T U O B Z
T P B E J R X R T D O B R
T L B E P R Q W T H O B H
T X B E B R P C T V O B P

Der einzige Affe, der übrigens für dieses Beispiel gerade zur Verfügung stand, war ich selber, aber wo um alles in der Welt habe ich einen 26-flächigen Würfel hergenommen? Kollege Computer musse es mal wieder richten und einen Affen simulieren. Wer wissen will, wie das Beispiel erzeugt wurde, kann hier die einfache LibreOffice Calc Datei herunterladen: to-be-or-not-to-be.ods. Reale Affen scheinen übrigens weitaus krasser zu sein. So schreibt der Wikipedia-Artikel zum "Infinite Monkey Theorem":

Im Jahr 2003 berichteten Wissenschaftler und Studenten des Zoos von Paignton und der University of Plymouth in Devon in England, dass sie einen Monat lang eine Computertastatur in einem Käfig mit sechs Makaken platziert hatten: Die Affen hatten nichts Sinnvolles zustande gebracht: lediglich fünf Seiten, wobei die Texte hauptsächlich aus dem Buchstaben S bestanden. Die Affen hatten außerdem mit einem Stein auf die Tastatur eingeschlagen und sich über der Tastatur entleert.

Ein Simulationsprogramm

Aber was ist schon ein Shakespeare-Zitat gegen den ganzen Shakespeare. Zwar nicht die gesammelten Werke, die ich nicht in einer einzigen Datei gefunden habe, aber etwas deutlich größeres soll es schon sein: Den kompletten "Hamlet", heruntergeladen vom bereits oben genannten Link. Wenn man den Vorspann und Nachspann des Textes wegläßt, dann ist der Text 190000 Zeichen lang. Und da ich mich nicht auf Shakespeare-Texte beschränken wollte, lasse ich nicht nur 26 Großbuchstaben zu, sondern den gesamten Umfang eines Bytes, also 256 verschiedene Möglichkeiten pro Zeichenposition.

Das Beispiel ist momentan (wir schreiben das Jahr 2018) etwas zu groß, um es wie oben in einer Tabellenkalkulation zu simulieren. Es ist aber immer noch so einfach, dass es schnell in der Sprache "C" programmiert ist.

/* Project: Infinite Monkeys
 * File:   infinite_monkeys.c
 * Author: Thomas Kneisel
 *
 * Created on 28. Januar 2018, 20:33
 */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main(int argc, char** argv) {
	unsigned char c, *filename, *sourceBuffer, *resultBuffer;
	int i, filelength, correct, generation;
	FILE *fp;

	/* get filename from comandline*/
	if (argc != 2) {
		printf("infinite_monkeys filename\n");
		exit(1);
	}
	filename = argv[1];

	/* open text file */
	fp = fopen(filename, "r");
	if (fp == 0) {
		printf("Cannot open file \"%s\"\n", filename);
		exit(1);
	}

	/* count the characters in the file */
	filelength = 0;
	while (!feof(fp)) {
		c = fgetc(fp);
		filelength++;
	}
	printf("file \"%s\", length %d characters\n", filename, filelength);

	/* create a buffer in RAM */
	sourceBuffer = malloc(filelength * sizeof (unsigned char));
	resultBuffer = malloc(filelength * sizeof (unsigned char));
	if ((sourceBuffer == 0) || (resultBuffer == 0)) {
		printf("out of memory\n");
		exit(1);
	}

	/* read the content of the file */
	rewind(fp);
	for (int i = 0; i < filelength; i++) {
		sourceBuffer[i] = fgetc(fp);
	}

	/* initialise result with random values */
	srand(time(NULL));
	generation = 1;
	correct = 0;
	for (int i = 0; i < filelength; i++) {
		resultBuffer[i] = rand() % 256;
		if (resultBuffer[i] == sourceBuffer[i])
			correct++;
	}
	printf("generation\tcorrect\ttotal\tpercentage\n");
	printf("%d\t%d\t%d\t%f\n", generation, correct, filelength,
			(float) correct / (float) filelength * 100.);

	/* improve the result by a new randowm value for all non-matching cahracters
	   until all characters are matching
	 */
	do {
		correct = 0;
		for (int i = 0; i < filelength; i++) {
			if (resultBuffer[i] != sourceBuffer[i])
				resultBuffer[i] = rand() % 256;
			if (resultBuffer[i] == sourceBuffer[i])
				correct++;
		}
		generation++;
		printf("%d\t%d\t%d\t%f\n", generation, correct, filelength,
				(float) correct / (float) filelength * 100.);
	} while (correct != filelength);

	/* release the text buffer and close the file */
	free(sourceBuffer);
	fclose(fp);

	return (EXIT_SUCCESS);
}

Kopieren sie den Quelltext in eine Datei mit dem Namen infinite_monkeys.c und übersetzen sie das Programm mit einem C-Compiler ihrer Wahl. Mit dem weit verbreiteten und kostenlosen GNU Compiler geht das beispielsweise mit:

gcc infinite_monkeys.c -o infinite_monkeys

Wenn das fehlerfrei funktioniert haben sollte, kann das Programm gestartet werden. Das Argument hinter dem Programmnamen ist die Textdatei mit dem Hamlet.

./infinite_monkeys 1524-0.txt

Die Ausgabe am Bildschirm dürfte ungefähr wie folgt aussehen:

file "1524-0.txt", length 180166 characters
generation	correct	total	percentage
1	735	180166	0.407957
2	1388	180166	0.770401
3	2045	180166	1.135064
4	2720	180166	1.509719
5	3413	180166	1.894364
6	4142	180166	2.298991
7	4818	180166	2.674200
8	5497	180166	3.051075
9	6198	180166	3.440161
10	6914	180166	3.837572

So geht es dann ziemlich lange weiter. Geschätze 3500 Zeilen weiter unten kommt das Ende. Weil das Programm mit (simuliertem) Zufall arbeitet, ergeben sich bei jedem Aufruf geringfügig andere Werte.

3550	180165	180166	99.999446
3552	180165	180166	99.999446
3553	180165	180166	99.999446
3554	180165	180166	99.999446
3555	180165	180166	99.999446
3556	180165	180166	99.999446
3557	180165	180166	99.999446
3558	180165	180166	99.999446
3559	180165	180166	99.999446
3560	180166	180166	100.0000002

Grafisch dargestellt ergibt die Zahlenwüste eine glatte Kurve:

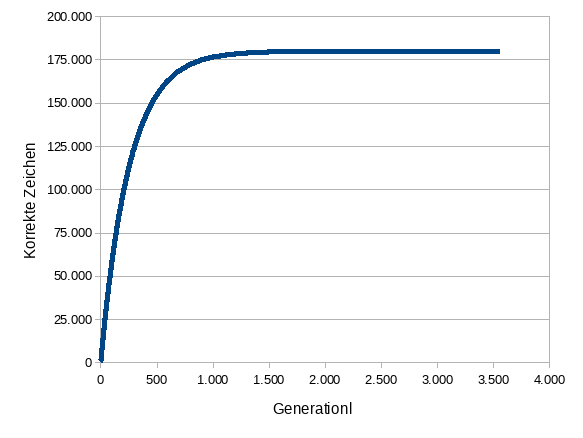
Wie Shakespeares "Hamlet" aus Zufall entsteht

Analytische Berechnung

Versuchen wir das etwas präziser in Formeln zu fassen. Es sei $n_{0}$ die Gesamtzahl der Zeichen im Text. Ausserdem sei $p$ die Wahrscheinlichkeit, dass bei einem einzelnen Zufallsexperiment ein einzelnes Zeichen den korrekten Wert annimmt. Im Falle von als Byte orientierten, also achtbittigen Daten gilt:

$p = \frac{1}{2^{8}} = \frac{1}{256}$

Unsere Erwartung ist, dass bereits in der ersten Generation eine gewisse Menge Zeichen ganz zufällig den korrekten Wert der jeweiligen Textposition annehmen. Diese Menge der falschen Zeichen reduziert sich voraussichtlich um den Erwartungswert:

${Δn}_{F} (1) = n_{F} (0) \cdot p$

also

$n_{F} (1) = n_{F} (0) - {Δn}_{F} (1) = n_{F} (0) - n_{F} (0) \cdot p = n_{F} (0) \cdot (1 - p)$

oder aber allgemeiner für den Schritt $i$ :

$n_{F} (i + 1) = n_{F} (i) \cdot (1 - p)$

Mit dem Wissen, dass die Zahl der korrekten Zeichen $n_{K}$ und der falschen Zeichen $n_{F}$ immer $n_{0}$ ergibt, können wir erstere berechnen:

$n_{K} (i) = n_{0} - n_{F} (i) Rekursive Berechnungsformeln sind ja ganz schön, aber man muss die gesamte Folge immer ausgehend vom Anfangswert Schritt für Schritt berechnen. Gibt es eine Möglichkeit die Werte "direkt" zu berechnen? Zunächst dachte ich, das Problem irgendwie als geometrische Reihe zu betrachten und dann die Summenformel darauf loszulassen. Google sei Dank bin ich aber auf folgenden Artikel gestoßen: Dr. Norbert Röhrl: Kapitel 14 Lineare Differenzengleichungen aus dem ich lernte, dass es sich bei meinem Problem um eine homogene linearen Differenzengleichung erster Ordnung mit konstanten Koeffizienten handelt. Mit denen hatte ich bislang noch nichts zu tun, aber die Lösung erfolgt sehr ählich wie bei linearen Differentialgleichungen. Zunächst die Differenzengleichung, die man durch Umstellung obiger Gleichung für n_{F} erhält:$

$n_{F} (i + 1) + (p - 1) \cdot n_{F} (i) = 0 Ähnlich wie bei Differentialgleichungen, bei denen die Exponentialfunktion immer zur Lösung führt, gibt es auch hier eine Silberkugel, die immer trifft. Der Ansatz lautet: λ^{i}$

Eingesetzt in die Differenzengleichung erhalten wir:

$λ^{i + 1} + (p - 1) \cdot λ^{i} = 0$

Zur Bestimmung des Eigenwertes $λ$ muss man nur noch genau dieses fleißig aus der Gleichung herauskürzen.

$λ + p - 1 = 0$

$λ = 1 - p$

Die Gesamtlösung ergibt sich aus einer Linearkombination aller Ansatzfunktionen. Da wir nur einen einzigen Eigenwert gefunden haben, ist das recht übersichtlich, wir erhalten:

$n_{F} (i) = k \cdot λ^{i}$

Die Konstante $k$ wird aus der Anfangsbedingung gewonnen und das war es dann auch schon:

$n_{F} (0) = n_{0}$

$k \cdot λ^{0} = n_{0}$

$k = n_{0}$

Endlich die Lösungsformeln:

$n_{F} (i) = n_{0} \cdot {(1 - p)}^{i}$

$n_{G} (i) = n_{0} - n_{0} \cdot {(1 - p)}^{i}$

Richtig gerechnet?

Vergleichen wir das Ergebnis unseres numerischen Experiments mit den Formeln.

hier fehlt ein Bild...

Numerisches Experiment und stochastisches Modell im Vergleich

Kritik

Kritik am Infinite Monkey Theorem

Gegen das Infinite Monkey Theorem ist für sich genommen grundsätzlich nichts einzuwenden, sofern man es nicht als Argument gegen die Evolutionstheorie benutzt. Denn es suggeriert, die Evolution hätte

entweder die Vielfalt des Lebens in einem einzigen riesigen Schritt erzeugt
oder sie wurstelt ohne Gedächtnis vor sich hin.

Da beides nicht funktionieren kann, müsse es dann ein intelligenter Schöpfer gewesen sein. Der entweder

alles auf einen Schlag erschaffen hat oder
ständig steuernd in seine Schöpfung einggeriffen habe, ja eingreifen haben müsse.

Nebenbei bemerkt: Einen Schöpfer stelle ich nicht grundsätzlich in Frage. Aber einer, der andauernd in seine eigene Schöpfung eingreifen muss, indem er jedes einzelne Viech mühsam einzeln herstellt, dem fehlt es an Größe.

Kritik am Evolutionsmodell

Dennoch ist auch Kritik an dem vorgestellten Modell der Evolution angebracht, denn es liegt weit von der Wirklichkeit entfernt.

Die Evolution weiß nicht, was richtig und falsch ist. Einzelne, bereits getätigte Treffer kann sie nicht als solche erkennen und von weiteren Veränderungen ausnehmen. Das liegt einerseits daran, dass sie kein Mittel besitzt, zu erkennen, dass die 178000. oder irgendeine andere Textposition mit dem Original übereinstimmt. Und es liegt auch daran, dass es gar kein Original gibt.
Genau deswegen zerschießt die reale Evolution positive Zwischenergebnisse.

Stehen wir damit wieder am Anfangspunkt? Im folgenden werden wir untersuchen, was passiert, wenn wir einige unserer Positionen aufgeben. Es wird sich zeigen, dass wir damit nicht auf das Niveau eines tippenden Affen heruntersinken. Lesen sie weiter im zweiten Teil "Ein besonders einfaches Modell"